Date: October 6, 2025

Stack safe ANF conversion in C++ using defunctionalization

Recently I’ve been interested in the idea of writing compilers for functional programming languages in C++. C++ has the most up-to-date bindings for generating LLVM IR, and is the most commonly used language for compiler jobs. So I wanted to get some project experience with C++, and what better way than to write a small compiler for a functional language in it?

The biggest issue with using C++ for this task is that compilers for functional languages tend to heavily use recursion for rewriting trees, and with C++ we need to be careful not to overflow the stack. While with most of the passes I can get by with visitors and explicit heap allocated stack structures like std::stack or std::vector, the thing that stumped me the most was ANF conversion.

What is ANF conversion? Well, one difference between a compiler for a functional language and an imperative one is that functional compilers have higher order functions which must be transformed away by the compiler before it can be lowered to LLVM. We also want the compiler to apply specific transformations related to functional programming languages like function uncurrying, argument flattening, etc.

This calls for another intermediate language between the abstract syntax tree and LLVM IR, which still preserves the tree structure for nested functions, if statements, and join points (which are like basic blocks but with arguments), but otherwise disallows nested expressions. So something that is expressed as 1 + 2 * 3 in the abstract syntax tree would be represented like:

let tmp1 = 2 * 3 in
let tmp2 = 1 + tmp1 in
tmp2

This representation is called A-normal form or ANF for short. ANF conversion is the process of converting the abstract syntax tree into A-normal form. The image below shows the process of ANF conversion for a expression in a language with if, lambda, apply, and binary operator expressions:

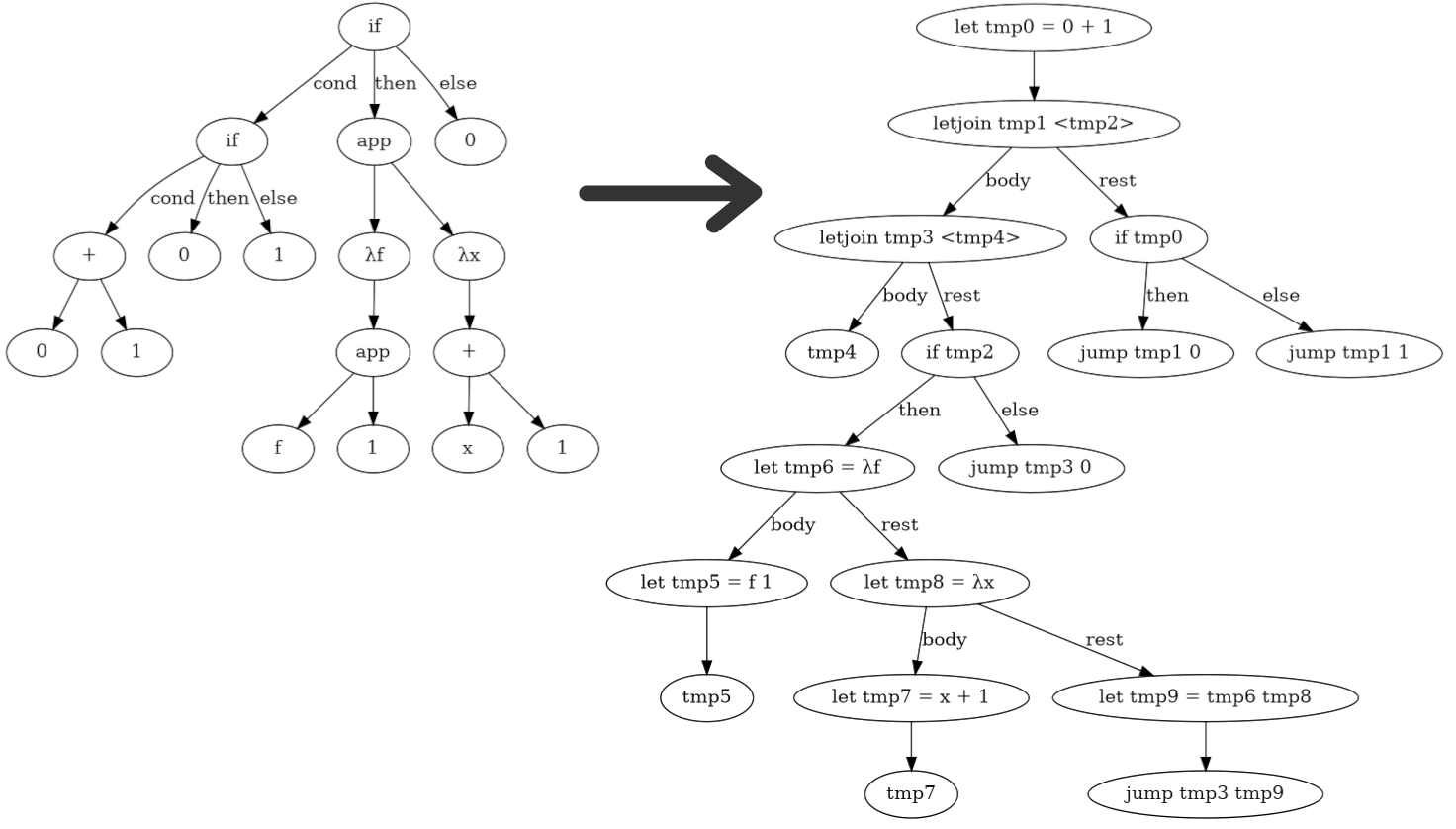
How would we implement this transformation? Lets look at a sample example for if expressions. If we have 1 + if 0 + 1 then 1 + 2 else 2 * 3 what would the output look like?

let tmp0 = 0 + 1 in
let%join tmp1 <tmp2> =
  let tmp3 = 1 + tmp2 in
  tmp3
in
if tmp0 then
  let tmp5 = 1 + 2 in
  jump tmp1 tmp5
else
  let tmp6 = 2 * 3 in
  jump tmp1 tmp6

The body of the join point contains the “rest” of the code that uses the value of the if expression (stored in the join point’s argument tmp2). The then and else expressions are recursively converted into ANF and linked to a jump expression at the end. The psuedocode for what we want this transformation to look like is shown below:

result_condition = recursively convert condition expression
let%join joinName <slot>
  [rest of the computation using slot as the value of the if expression]
in
if result_condition then
  result_then = recursively convert then expression
  jump joinName result_then
else
  result_else = recursively convert else expression
  jump joinName result_else

Because we have a problem where we want to expand the rest of the computation, we want to pass in a continuation into the conversion function. The continuation will take as a parameter a value denoting the result of the expression, and return the result of ANF converting the rest of the program. This is what this looks like in C++ (k is a member of the AnfConvertVisitor class and refers to the continuation):

std::unique_ptr<Exp> AnfConvertVisitor::operator()(ast::IfExp &exp) {
  return exp.cond->convert([&thenBranch = *exp.then, &elseBranch = *exp.els,
                            &k = k](Value condValue) {
    auto joinName = fresh();
    auto slot = fresh();
    return make(JoinExp{
        .name = joinName,
        .slot = std::optional{slot},
        .body = k(VarValue{slot}),
        .rest = make(IfExp{
            .cond = condValue,
            .thenBranch = thenBranch.convert([&joinName](Value value) {
              return make(JumpExp{joinName, std::optional{std::move(value)}});
            }),
            .elseBranch = elseBranch.convert([&joinName](Value value) {
              return make(JumpExp{joinName, std::optional{std::move(value)}});
            })})});
  });
}

The if else case is the hardest case to handle; the other cases are pretty easy. However, we should take a step back. Just from looking at the if else example it should be clear that the conversion is happening recursively. We don’t want this because if we pass in a larger AST, then we can get stack overflows.

What we want to do instead is to convert this recursion into a loop. Because all recursive uses will have to be eliminated, that includes the continuation call since that is also recursive. This means that the higher order function k will have to be eliminated through the process of defunctionalization.

Because defunctionalization is a pretty involved process, we want to do this in a language better suited for the task. You could use any functional language with guaranteed tail call elimination like Scheme, Haskell, OCaml, etc. but for this I chose Standard ML because it doesn’t have syntax sugar like do notation or let binding syntax, making it slightly easier to identify closures.

Let’s start off by writing the basic recursive implementation for ANF conversion in Standard ML:

local
  fun go exp k =
    case exp of
      L.Int i => k (Int i)
    | L.Var v => k (Var v)
    | L.Lam (v, body) =>
        let
          val body = go body Halt
          val f = fresh "f"
        in
          Fun (f, [v], body, k (Var f))
        end
    | L.App (f, x) =>
        go f (fn f =>
        go x (fn x =>
        case f of
          Var f => let val r = fresh "r" in App (r, f, [x], k (Var r)) end
        | _ => raise Fail "must apply named value"))
    | L.Bop (bop, x, y) =>
        go x (fn x =>
        go y (fn y =>
        let val r = fresh "r"
        in Bop (r, bop, x, y, k (Var r))
        end))
    | L.If (c, t, f) =>
        go c (fn c =>
          let
            val (j, p) = (fresh "j", fresh "p")
            val jump = fn p => Jump (j, SOME p)
          in
            Join (j, SOME p, k (Var p), If (c, go t jump, go f jump))
          end)
in val convert = fn exp => go exp Halt
end

Although we pass in a continuation k into the conversion function, this conversion function is not in continuation passing style form. In continuation passing style, all function calls are always in tail position, or in other words, at the very end of the function. But in this function, we call k and use its return value afterwards, which means it is not called in tail position. So the first thing we need to do is convert go to be in proper continuation passing style form. We do that by having the continuation k itself take in a continuation for what to do with the result ANF expression. We call this continuation k' and it takes an ANF expression as a parameter and the result. Then, we thread k' into the go function as well so that when we need to call k we have a k' ready to pass into it.

local
  fun go (exp: L.exp) (k': exp -> exp) (k: value * (exp -> exp) -> exp) : exp =
    case exp of
      L.Int i => k (Int i, k')
    | L.Var v => k (Var v, k')
    | L.Lam (v, body) =>
        let
          val k' = fn body =>
            let val f = fresh "f"
            in k (Var f, fn rest => k' (Fun (f, [v], body, rest)))
            end
        in
          go body k' (fn (value, k') => k' (Halt value))
        end
    | L.App (f, x) =>
        go f k' (fn (f, k') =>
        go x k' (fn (x, k') =>
        case f of
          Var f =>
            let val r = fresh "r"
            in k (Var r, fn rest => k' (App (r, f, [x], rest)))
            end
        | _ => raise Fail "must apply named value"))
    | L.Bop (bop, x, y) =>
        go x k' (fn (x, k') =>
        go y k' (fn (y, k') =>
        let val r = fresh "r"
        in k (Var r, fn rest => k' (Bop (r, bop, x, y, rest)))
        end))
    | L.If (c, t, f) =>
        go c k' (fn (c, k') =>
          let
            val (j, p) = (fresh "j", fresh "p")
            val jump = fn (v, k') => k' (Jump (j, SOME v))
            val go' = fn e => fn f => go e f jump
          in
            k (Var p, fn rest =>
              go' t (fn t =>
              go' f (fn f =>
              k' (Join (j, SOME p, rest, If (c, t, f))))))
          end)
in
  val convertCPS: L.exp -> exp = fn e =>
    go e (fn a => a) (fn (v, k) => k (Halt v))
end

This function is completely tail recursive, but we cannot port this directly to C++. Even if we use Clang and GCC’s musttail attribute for tail call optimization, that optimization can only be applied for tail calls with the exact same type signature as the function itself, which is not the case here. So we still need to do defunctionalization.

The first step to defunctionalization is to identify the types of closures that need to be lowered. For our ANF conversion function we have two types: k' which refers to closures with the type exp -> exp, and k for the type value * (exp -> exp) -> exp. We create two algebraic data types, K' for representing closures with the type of k', and K representing closures with the type of k. We then create two functions applyK', and applyK that will be used in place of calling a continuation with the given arguments. The exp -> exp argument to k is also translated to a K' type since we are replacing all higher order functions with the defunctionalized version. This is what it looks like so far, with ... representing the parts that haven’t been filled out yet:

datatype K' =
  ...
and K =
  ...

fun go (exp: L.exp) (k': K') (k: K) : exp =
  ...
and applyK' (k' : K') (exp: exp) : exp =
  ...
and applyK (k : K) (value: value) (k': K') : exp =
  ...

Now we have to identify all the closures for each closure type. This means looking for all expressions in the form fn _ =>. Starting with k', there are two closures in the Lam branch:

| L.Lam (v, body) =>
    let
      val k' = (* k' closure 1 *) fn body =>
        let val f = fresh "f"
        in k (Var f, (* k' closure 2 *) fn rest => k' (Fun (f, [v], body, rest)))
        end
    in
      go body k' (fn (value, k') => k' (Halt value))
    end

The second closure for k' is inside the first closure but we still have to count it.

We also have to identify all of the free variables for each closure. Free variables are variables that are defined outside the closure but referred to inside the closure. For the first closure, variables k, k', and v are free (marked with the (**) in the code below):

fn body =>
  let val f = fresh "f"
  in
    (**) k (Var f, fn rest => (**) k' (Fun (f, [(**) v], body, rest)))
  end

For the second closure, k', f, v, and body are free:

fn rest => (**) k' (Fun ((**) f, [(**) v], (**) body, rest))

For both closures, we make a data constructor for the K' type that contains the free variables for the respective closures:

datatype K' =
  K'_Lam1 of {k': K', k: K, v: string}
| K'_Lam2 of {k': K', f: string, v: string, body: exp}
...

For the App branch, there is one k' closure with free variables k', r, f, and x:

fn rest => (**) k' (App ((**) r, (**) f, [(**) x], rest))

We add another constructor to K':

| K'_App1 of {r: string, f: string, x: value, k': K'}

For the Bop branch, there is one k' closure with free variables k', r, bop, x, and y:

fn rest => (**) k' (Bop ((**) r, (**) bop, (**) x, (**) y, rest))

| K'_Bop1 of {r: string, bop: L.bop, x: value, y: value, k': K'}

For the If branch, we have three k' closures:

| L.If (c, t, f) =>
    go c k' (fn (c, k') =>
      let
        val (j, p) = (fresh "j", fresh "p")
        val jump = fn (v, k') => k' (Jump (j, SOME v))
        val go' = fn e => fn f => go e f jump
      in
        k (Var p, (* closure 1 *) fn rest =>
          go' t (* closure 2 *) (fn t =>
          go' f (* closure 3 *) (fn f =>
          k' (Join (j, SOME p, rest, If (c, t, f))))))
      end)

Note that when counting the closures for this branch, we ignore the closures in go' because go' e f is just a alias for go e f jump so the definition of go' is not necessary and can be inlined away.

The first closure has free variables t, f, k', j, p, and c:

fn rest =>
  go' (**) t (fn t =>
  go' (**) f (fn f =>
  (**) k' (Join ((**) j, SOME (**) p, rest, If ((**) c, t, f)))))

Since t and f are shadowed here we are referring to the AST expressions, not the converted ANF expressions.

The second closure has free variables f, k', j, p, rest, and c:

fn t =>
  go' (**) f (fn f =>
  (**) k' (Join ((**) j, SOME (**) p, (**) rest, If ((**) c, t, f))))

And the third closure has free variables k', j, p, rest, c, and t:

fn f =>
  (**) k' (Join ((**) j, SOME (**) p,  (**) rest, If ((**) c, (**) t, f)))

For this closure, t refers to the converted ANF expression instead of the AST expression.

This results in three new data constructors for K':

| K'_If1 of {t: L.exp, f: L.exp, k': K', j: string, p: string, c: value}
| K'_If2 of {f: L.exp, k': K', j: string, p: string, c: value, rest: exp}
| K'_If3 of {t: exp, k': K', j: string, p: string, c: value, rest: exp}

Finally, convertCPS has a (fn a => a) that is passed as a k' closure. Since that has no free variables, the constructor doesn’t contain anything:

| K'_Convert (* Initial fn a => a passed into go *)

That’s it for the k' closures. Now we have to add the data constructors for the k closures. We are looking for closures that have a tuple as a parameter now.

The first one is in the Lam branch with no free variables:

go body k' (fn (value, k') => k' (Halt value))

The App branch has two k closures with free variables x, k for the first closure, and f, k for the second closure:

| L.App (f, x) =>
    go f k' (* closure 1 *) (fn (f, k') =>
    go x k' (* closure 2 *) (fn (x, k') =>
    case f of
      Var f =>
        let val r = fresh "r"
        in k (Var r, fn rest => k' (App (r, f, [x], rest)))
        end
    | _ => raise Fail "must apply named value"))

The Bop branch has two k closures with free variables y, bop, k for the first closure, and x, bop, k for the second closure:

| L.Bop (bop, x, y) =>
    go x k' (* closure 1 *) (fn (x, k') =>
    go y k' (* closure 2 *) (fn (y, k') =>
    let val r = fresh "r"
    in k (Var r, fn rest => k' (Bop (r, bop, x, y, rest)))
    end))

And the If branch has two k closures with free variables t, f, k for the first closure and j for the second closure:

| L.If (c, t, f) =>
    go c k' (* closure 1 *) (fn (c, k') =>
      let
        val (j, p) = (fresh "j", fresh "p")
        val jump = (* closure 2 *) fn (v, k') => k' (Jump (j, SOME v))
        val go' = fn e => fn f => go e f jump
      in
        k (Var p, fn rest =>
          go' t (fn t =>
          go' f (fn f =>
          k' (Join (j, SOME p, rest, If (c, t, f))))))
      end)

In convertCPS, we pass in a (fn (v, k) => k (Halt v)) closure which is exactly the same as the closure passed in the Lam1 branch so we don’t need to add another constructor.

Now that we filled out the constructors for K and K' we can rewrite the cases in go so that all calls to k (a, b) are replaced with applyK k a b, all calls to k' a are replaced with applyK' k' a, and all closures passed in are replaced with the corresponding data constructor for k or k'.

fun go (exp: L.exp) (k': K') (k: K) : exp =
  case exp of
    L.Int i => applyK k (Int i) k'
  | L.Var v => applyK k (Var v) k'
  | L.Lam (v, body) => go body (K'_Lam1 {k' = k', k = k, v = v}) K_Lam1
  | L.App (f, x) => go f k' (K_App1 {x = x, k = k})
  | L.Bop (bop, x, y) => go x k' (K_Bop1 {y = y, bop = bop, k = k})
  | L.If (c, t, f) => go c k' (K_If1 {t = t, f = f, k = k})

We don’t have to care that closures are nested in each other, we only pass in the corresponding data constructor for the topmost closure. The nested closures will be handled in the body of applyK or applyK'.

Now we do the same thing for applyK' and applyK.

Starting with applyK', the closure for K'_Convert is (fn a => a), which becomes:

and applyK' K'_Convert exp = exp

The closure for the first closure in the Lam branch is:

fn body =>
  let val f = fresh "f"
  in k (Var f, fn rest => k' (Fun (f, [v], body, rest)))
  end

So the corresponding applyK' branch becomes:

| applyK' (K'_Lam1 {k', k, v}) body =
    let val f = fresh "f"
    in applyK k (Var f) (K'_Lam2 {k' = k', f = f, v = v, body = body})
    end

The nested second closure in the Lam branch is:

fn rest => k' (Fun (f, [v], body, rest))

Which becomes:

| applyK' (K'_Lam2 {k', f, v, body}) rest =
    applyK' k' (Fun (f, [v], body, rest))

Because each closure case only handles its own body ignoring nesting, the total lines of code for the defunctionalized case isn’t significantly greater than the normal tail recursive one. Of course, the defunctionalized version is much harder to understand. The final code after handling all of the applyK and applyK' cases is shown below:

local
  fun go (exp: L.exp) (k': K') (k: K) : exp =
    case exp of
      L.Int i => applyK k (Int i) k'
    | L.Var v => applyK k (Var v) k'
    | L.Lam (v, body) => go body (K'_Lam1 {k' = k', k = k, v = v}) K_Lam1
    | L.App (f, x) => go f k' (K_App1 {x = x, k = k})
    | L.Bop (bop, x, y) => go x k' (K_Bop1 {y = y, bop = bop, k = k})
    | L.If (c, t, f) => go c k' (K_If1 {t = t, f = f, k = k})
  and applyK' K'_Convert exp = exp
    | applyK' (K'_Lam1 {k', k, v}) body =
        let val f = fresh "f"
        in applyK k (Var f) (K'_Lam2 {k' = k', f = f, v = v, body = body})
        end
    | applyK' (K'_Lam2 {k', f, v, body}) rest =
        applyK' k' (Fun (f, [v], body, rest))
    | applyK' (K'_App1 {r, f, x, k'}) rest =
        applyK' k' (App (r, f, [x], rest))
    | applyK' (K'_Bop1 {r, bop, x, y, k'}) rest =
        applyK' k' (Bop (r, bop, x, y, rest))
    | applyK' (K'_If1 {t, f, k', j, p, c}) rest =
        go t (K'_If2 {f = f, k' = k', j = j, p = p, c = c, rest = rest})
          (K_If2 {j = j})
    | applyK' (K'_If2 {f, k', j, p, c, rest}) t =
        go f (K'_If3 {t = t, k' = k', j = j, p = p, c = c, rest = rest})
          (K_If2 {j = j})
    | applyK' (K'_If3 {t, k', j, p, c, rest}) f =
        applyK' k' (Join (j, SOME p, rest, If (c, t, f)))
  and applyK K_Lam1 value k' =
        applyK' k' (Halt value)
    | applyK (K_App1 {x, k}) f k' =
        go x k' (K_App2 {f = f, k = k})
    | applyK (K_App2 {f, k}) x k' =
        (case f of
           Var f =>
             let val r = fresh "r"
             in applyK k (Var r) (K'_App1 {r = r, f = f, x = x, k' = k'})
             end
         | _ => raise Fail "must apply named value")
    | applyK (K_Bop1 {y, bop, k}) x k' =
        go y k' (K_Bop2 {x = x, bop = bop, k = k})
    | applyK (K_Bop2 {x, bop, k}) y k' =
        let
          val r = fresh "r"
        in
          applyK k (Var r) (K'_Bop1 {r = r, bop = bop, x = x, y = y, k' = k'})
        end
    | applyK (K_If1 {t, f, k}) c k' =
        let
          val (j, p) = (fresh "j", fresh "p")
        in
          applyK k (Var p) (K'_If1
            {t = t, f = f, k' = k', j = j, p = p, c = c})
        end
    | applyK (K_If2 {j}) v k' =
        applyK' k' (Jump (j, SOME v))
in val convertDefunc: L.exp -> exp = fn e => go e K'_Convert K_Lam1
end

There is one final thing we want to do before translating back to C++. Let’s look at the datatypes for K and K' again:

datatype K' =
  K'_Convert (* Initial fn a => a passed into go *)
| K'_Lam1 of {k': K', k: K, v: string}
| K'_Lam2 of {k': K', f: string, v: string, body: exp}
| K'_App1 of {r: string, f: string, x: value, k': K'}
| K'_Bop1 of {r: string, bop: L.bop, x: value, y: value, k': K'}
| K'_If1 of {t: L.exp, f: L.exp, k': K', j: string, p: string, c: value}
| K'_If2 of {f: L.exp, k': K', j: string, p: string, c: value, rest: exp}
| K'_If3 of {t: exp, k': K', j: string, p: string, c: value, rest: exp}
and K =
  K_Lam1
| K_App1 of {x: L.exp, k: K}
| K_App2 of {f: value, k: K}
| K_Bop1 of {y: L.exp, bop: L.bop, k: K}
| K_Bop2 of {x: value, bop: L.bop, k: K}
| K_If1 of {t: L.exp, f: L.exp, k: K}
| K_If2 of {j: string}

Inside almost every data constructor for K', it has another value of type K' inside of it as a free variable. Data constructors for K mostly have K as a free variable as well. If we model this in C++, this would become a linked-list chain of unique_ptrs which is not very efficient and harder to work with.

Instead, we can remove all of the recursive free variables for K' and model it as a stack of frames. The stack after popping the topmost frame off of it is the free variable k' for the topmost continuation. Pushing a frame to the stack is the same as creating a closure that wraps the existing closure as a free variable. The K type can also be modeled as a stack in the same way. The cases K'_Convert and K_Lam1 are the cases where the K or K' stack is empty.

This stack method can be efficiently modeled in C++ as a dynamically resizable array like std::vector. Right now we will model the stack as a list of frames but we will translate it to a vector when converting to C++. Here are the transformed types for K and K':

datatype K'Frame =
  K'_Lam1 of {k: K, v: string}
| K'_Lam2 of {f: string, v: string, body: exp}
| K'_App1 of {r: string, f: string, x: value}
| K'_Bop1 of {r: string, bop: L.bop, x: value, y: value}
| K'_If1 of {t: L.exp, f: L.exp, j: string, p: string, c: value}
| K'_If2 of {f: L.exp, j: string, p: string, c: value, rest: exp}
| K'_If3 of {t: exp, j: string, p: string, c: value, rest: exp}
and KFrame =
  K_App1 of {x: L.exp}
| K_App2 of {f: value}
| K_Bop1 of {y: L.exp, bop: L.bop}
| K_Bop2 of {x: value, bop: L.bop}
| K_If1 of {t: L.exp, f: L.exp}
| K_If2 of {j: string}
withtype K' = K'Frame list
and K = KFrame list

Now we rewrite the go function so that when we pass in a closure that wraps k or k', we push the frame with the non-recursive free variables to the stack. So something like K'_Lam1 {k' = k', k = k, v = v} becomes K'_Lam1 {k = k, v = v} :: k':

fun go (exp: L.exp) (k': K') (k: K) : exp =
  case exp of
    L.Int i => applyK k (Int i) k'
  | L.Var v => applyK k (Var v) k'
  | L.Lam (v, body) => go body (K'_Lam1 {k = k, v = v} :: k') []
  | L.App (f, x) => go f k' (K_App1 {x = x} :: k)
  | L.Bop (bop, x, y) => go x k' (K_Bop1 {y = y, bop = bop} :: k)
  | L.If (c, t, f) => go c k' (K_If1 {t = t, f = f} :: k)

[] is substituted for K_Lam1 and K'_Convert.

When rewriting the applyK and applyK' functions, we destruct the K or K' stack and the rest of the list is the free variable for k or k'. So something like K'_Lam2 {k', f, v, body} becomes K'_Lam2 {f, v, body} :: k' when pattern matching:

and applyK' [] (exp: exp) = exp
  | applyK' (K'_Lam1 {k, v} :: k') body =
      let val f = fresh "f"
      in applyK k (Var f) (K'_Lam2 {f = f, v = v, body = body} :: k')
      end
  | applyK' (K'_Lam2 {f, v, body} :: k') rest =
      applyK' k' (Fun (f, [v], body, rest))
  | applyK' (K'_App1 {r, f, x} :: k') rest =
      applyK' k' (App (r, f, [x], rest))
  | applyK' (K'_Bop1 {r, bop, x, y} :: k') rest =
      applyK' k' (Bop (r, bop, x, y, rest))
  | applyK' (K'_If1 {t, f, j, p, c} :: k') rest =
      go t (K'_If2 {f = f, j = j, p = p, c = c, rest = rest} :: k')
        [K_If2 {j = j}]
  | applyK' (K'_If2 {f, j, p, c, rest} :: k') t =
      go f (K'_If3 {t = t, j = j, p = p, c = c, rest = rest} :: k')
        [K_If2 {j = j}]
  | applyK' (K'_If3 {t, j, p, c, rest} :: k') f =
      applyK' k' (Join (j, SOME p, rest, If (c, t, f)))
and applyK [] value k' =
      applyK' k' (Halt value)
  | applyK (K_App1 {x} :: k) f k' =
      go x k' (K_App2 {f = f} :: k)
  | applyK (K_App2 {f} :: k) x k' =
      (case f of
         Var f =>
           let val r = fresh "r"
           in applyK k (Var r) (K'_App1 {r = r, f = f, x = x} :: k')
           end
       | _ => raise Fail "must apply named value")
  | applyK (K_Bop1 {y, bop} :: k) x k' =
      go y k' (K_Bop2 {x = x, bop = bop} :: k)
  | applyK (K_Bop2 {x, bop} :: k) y k' =
      let val r = fresh "r"
      in applyK k (Var r) (K'_Bop1 {r = r, bop = bop, x = x, y = y} :: k')
      end
  | applyK (K_If1 {t, f} :: k) c k' =
      let val (j, p) = (fresh "j", fresh "p")
      in applyK k (Var p) (K'_If1 {t = t, f = f, j = j, p = p, c = c} :: k')
      end
  | applyK (K_If2 {j} :: _) v k' =
      applyK' k' (Jump (j, SOME v))

Finally, convertDefunc becomes val convertDefunc: L.exp -> exp = fn e => go e [] [] since it is called with both stacks empty initially.

The first thing when translating our Standard ML code to C++ is translating the algebraic data types for the continuations. This can be done by encoding every data constructor as a C++ struct, and encoding KFrame and K2Frame as a std::variant of the structs. Then K is an alias for a std::vector of KFrames and K2 is an alias for a std::vector of K2Frames. The translated code for the data types is shown below:

struct KFrame;
struct K2Frame;

using K = std::vector<KFrame>;
using K2 = std::vector<K2Frame>;

struct K2_Lam1 {
  K k;
  std::string v;
};

struct K2_Lam2 {
  std::string f, v;
  std::unique_ptr<Exp> body;
};

struct K2_App1 {
  std::string r, f;
  Value x;
};

struct K2_Bop1 {
  std::string r;
  ast::Bop bop;
  Value x, y;
};

struct K2_If1 {
  ast::Exp &t;
  ast::Exp &f;
  std::string j, p;
  Value c;
};

struct K2_If2 {
  ast::Exp &f;
  std::string j, p;
  Value c;
  std::unique_ptr<Exp> rest;
};

struct K2_If3 {
  std::unique_ptr<Exp> t;
  std::string j, p;
  Value c;
  std::unique_ptr<Exp> rest;
};

struct K2Frame : public std::variant<K2_Lam1, K2_Lam2, K2_App1, K2_Bop1, K2_If1,
                                     K2_If2, K2_If3> {
  using variant::variant;
};

struct K_App1 {
  ast::Exp &x;
};

struct K_App2 {
  Value f;
};

struct K_Bop1 {
  ast::Exp &y;
  ast::Bop bop;
};

struct K_Bop2 {
  Value x;
  ast::Bop bop;
};

struct K_If1 {
  ast::Exp &t;
  ast::Exp &f;
};

struct K_If2 {
  std::string j;
};

struct KFrame
    : public std::variant<K_App1, K_App2, K_Bop1, K_Bop2, K_If1, K_If2> {
  using variant::variant;
};

Now we need to encode the three tail recursive functions applyK, applyK' and go into a single loop body. We do this by writing an infinite loop and having a switch inside that dispatches to the right label:

std::unique_ptr<Exp> convert(ast::Exp &root) {
  // ... Combined parameters for apply_k2, apply_k, and go normalized ...

  enum { APPLY_K2, APPLY_K, GO } dispatch = GO;

  while (true) {
    switch (dispatch) {
    case APPLY_K2: {
      // ... translated code for function `applyK'` ...
      break;
    }
    case APPLY_K: {
      // ... translated code for function `applyK` ...
      break;
    }
    case GO: {
      // ... translated code for function `go` ...
      break;
    }
    }
  }
  return nullptr;
}

When tail calling, the function frame in the stack gets popped before jumping to the next function, so everything outside of the parameters to the tail call is “forgotten”. Because of that, we only need to define a union of all function parameters as variables outside the loop and when doing a tail call we destructively overwrite the variables that are the parameters and set the dispatch to the label of the next function.

• go takes in a ast::Exp* (we do not need to own the passed in AST expression), K, and K2
• applyK' takes in a K2 and a std::unique_ptr<anf::Exp>
• applyK takes in a K, anf::Value, and K2

The union of these parameters is a ast::Exp*, K, K2, std::unique_ptr<anf::Exp>, and a Value. So these variables are defined outside the infinite loop:

ast::Exp *go_exp = &root;
std::unique_ptr<anf::Exp> k2_exp;
K k;
K2 k2;
Value value;

Now to handle the cases for applyK, applyK', and go. Let’s start with go. The body for go simply visits the go_exp variable and handles every possible expression type:

case GO:
  std::visit(
      overloaded{
          [&](ast::IntExp &exp) {
            value = IntValue{exp.value};
            dispatch = APPLY_K;
          },
          [&](ast::VarExp &exp) {
            value = VarValue{exp.name};
            dispatch = APPLY_K;
          },
          // ... rest of the cases ...
      },
      *go_exp);
  break;

The first two cases are filled in, which correspond to the equivalent code in Standard ML:

  L.Int i => applyK k (Int i) k'
| L.Var v => applyK k (Var v) k'

k and k' are not changed in the function so they are not modified. The value variable is overwritten to IntValue or VarValue. Then we set dispatch to APPLY_K to simulate “calling” the applyK function since the switch statement will jump to the APPLY_K label when the code goes back around to the start of the loop.

Let’s apply the same process to the LamExp branch:

| L.Lam (v, body) => go body (K'_Lam1 {k = k, v = v} :: k') []

Since go is called recursively inside go, dispatch doesn’t need to be modified. However go_exp, k, and k' need to be modified. First we set go_exp to the expression’s body as a pointer. Then we swap the k variable with an empty vector and put its old value into oldK. We mentioned earlier that we will convert consing onto a list in Standard ML to pushing to the end of a vector in C++ so we move oldK into a K2_Lam1 type and then push it to the back of k2. We can do this without having to construct an intermediate struct using .emplace_back() and std::in_place_type:

[&](ast::LamExp &exp) {
  go_exp = exp.body.get();
  K oldK;
  k.swap(oldK);
  k2.emplace_back(std::in_place_type<K2_Lam1>, std::move(oldK),
                  exp.param);
},

The rest of the cases set go_exp to an expression child, push to the back of k and recurse with go:

| L.App (f, x) => go f k' (K_App1 {x = x} :: k)
| L.Bop (bop, x, y) => go x k' (K_Bop1 {y = y, bop = bop} :: k)
| L.If (c, t, f) => go c k' (K_If1 {t = t, f = f} :: k)

[&](ast::AppExp &exp) {
  go_exp = exp.fn.get();
  k.emplace_back(std::in_place_type<K_App1>, *exp.arg);
},
[&](ast::BopExp &exp) {
  go_exp = exp.arg1.get();
  k.emplace_back(std::in_place_type<K_Bop1>, *exp.arg2, exp.bop);
},
[&](ast::IfExp &exp) {
  go_exp = exp.cond.get();
  k.emplace_back(std::in_place_type<K_If1>, *exp.then, *exp.els);
},

For the applyK branch, we first check if k is empty. If it is, they we handle the empty list case:

applyK [] value k' = applyK' k' (Halt value)

Otherwise we pop the last frame of the vector and handle all the possible KFrame variants with std::visit. This is equivalent to the Standard ML code that pattern matches on the list of frames:

case APPLY_K: {
  if (k.empty()) {
    k2_exp = make(HaltExp{value});
    dispatch = APPLY_K2;
    continue;
  }
  auto frame = std::move(k.back());
  k.pop_back();
  std::visit(
      overloaded{
        // ... cases for KFrame variants ...
      },
      frame);
  break;
}

Now we start filling in each KFrame case. Starting with K_App1, it calls go with the frame’s expression and with K_App2 pushed to k:

[&](K_App1 &frame) {
  go_exp = &frame.x;
  k.emplace_back(std::in_place_type<K_App2>, std::move(value));
  dispatch = GO;
},

The K_App2 case pattern matches on the value passed into K_App2 to check if the function to apply is a named variable. To do this we use a nested std::visit over Values:

[&](K_App2 &frame) {
  std::visit(overloaded{[&](VarValue &f) {
                          auto r = fresh();
                          k2.emplace_back(
                              std::in_place_type<K2_App1>, r,
                              f.var, std::move(value));
                          value = VarValue{r};
                        },
                        [](auto &) {
                          throw std::runtime_error(
                              "must apply named value");
                        }},
             frame.f);
},

The K_Bop1 case calls go on the second parameter of the binop and pushes K_Bop2 to k:

[&](K_Bop1 &frame) {
  go_exp = &frame.y;
  k.emplace_back(std::in_place_type<K_Bop2>, std::move(value),
                 frame.bop);
  dispatch = GO;
},

The next two cases K_Bop2 and K_If1 push to k2 and recurse with applyK applied to the next k and a fresh variable. Since k was already popped before, it doesn’t have to be modified in these cases:

[&](K_Bop2 &frame) {
  auto r = fresh();
  k2.emplace_back(std::in_place_type<K2_Bop1>, r, frame.bop,
                  std::move(frame.x), std::move(value));
  value = VarValue{r};
},
[&](K_If1 &frame) {
  auto j = fresh();
  auto p = fresh();

  k2.emplace_back(std::in_place_type<K2_If1>, frame.t, frame.f,
                  std::move(j), p, std::move(value));
  value = VarValue{p};
},

We have to be careful to only assign value after moving the old value into the frame pushed into k2. Mixing up the order of modifications can cause the wrong value to be in the frame.

The last case K_If2 calls applyK' with a jump expression without pushing to k2. applyK' doesn’t use k, go_exp, or value but there is no need to clear out these variables; they will just be ignored in all the applyK' cases.

[&](K_If2 &frame) {
  k2_exp = make(JumpExp{.joinName = std::move(frame.j),
                        .slotValue = {std::move(value)}});
  dispatch = APPLY_K2;
},

The applyK' structure is similar to the structure of applyK in that it first checks and handles the case where k2 is empty and otherwise pops the last frame off of k2 and visits all variants of it. The main difference is that when k2 is empty the final ANF expression is returned, breaking out of the whole state machine loop.

case APPLY_K2: {
  if (k2.empty()) {
    return k2_exp;
  }
  auto frame = std::move(k2.back());
  k2.pop_back();
  std::visit(
      overloaded{
        // ... cases for K2Frame variants ...
      },
      frame);
  break;
}

In the first case K2_Lam1, applyK is called with the stack of frames held inside k2’s frame. The old value of k is discarded, which is fine because k is forgotten in the applyK' context anyway.

[&](K2_Lam1 &frame) {
  auto f = fresh();
  k = std::move(frame.k);
  value = VarValue{f};
  k2.emplace_back(std::in_place_type<K2_Lam2>, f, frame.v,
                  std::move(k2_exp));
  dispatch = APPLY_K;
},

The next three cases, K2_Lam2, K2_App1, and K2_Bop1 recursively calls itself with its expression wrapped in a larger expression that also contains parts of the variables in the frame.

[&](K2_Lam2 &frame) {
  k2_exp = make(FunExp{.name = std::move(frame.f),
                       .params = {std::move(frame.v)},
                       .body = std::move(frame.body),
                       .rest = std::move(k2_exp)});
},
[&](K2_App1 &frame) {
  k2_exp = make(AppExp{.name = std::move(frame.r),
                       .funName = std::move(frame.f),
                       .paramValues = {std::move(frame.x)},
                       .rest = std::move(k2_exp)});
},
[&](K2_Bop1 &frame) {
  k2_exp = make(BopExp{.name = std::move(frame.r),
                       .bop = frame.bop,
                       .param1 = std::move(frame.x),
                       .param2 = std::move(frame.y),
                       .rest = std::move(k2_exp)});
},

The next two cases K2_If1 and K2_If2 call go with k having only one element in the stack. This is done by clearing the old value of k and pushing a single frame.

[&](K2_If1 &frame) {
  go_exp = &frame.t;
  k2.emplace_back(std::in_place_type<K2_If2>, frame.f, frame.j,
                  std::move(frame.p), std::move(frame.c),
                  std::move(k2_exp));
  k.clear();
  k.emplace_back(std::in_place_type<K_If2>, frame.j);
  dispatch = GO;
},
[&](K2_If2 &frame) {
  go_exp = &frame.f;
  k2.emplace_back(std::in_place_type<K2_If3>, std::move(k2_exp),
                  frame.j, std::move(frame.p), std::move(frame.c),
                  std::move(frame.rest));
  k.clear();
  k.emplace_back(std::in_place_type<K_If2>, frame.j);
  dispatch = GO;
},

The last case, K2_If3 recursively calls itself with its expression wrapped in a join and a if expression containing the rest of the variables in the frame.

[&](K2_If3 &frame) {
  k2_exp = make(JoinExp{
      .name = std::move(frame.j),
      .slot = {std::move(frame.p)},
      .body = std::move(frame.rest),
      .rest = make(IfExp{.cond = std::move(frame.c),
                         .thenBranch = std::move(frame.t),
                         .elseBranch = std::move(k2_exp)})});
},

With this, the ANF conversion function is complete. The full code can be seen here.

There are some ways to optimize this implementation further. Instead of encoding the conversion as an infinite loop with a switch statement to dispatch to the right function, we could use computed goto to jump to the relevant label. We could also use clang’s musttail or Rust’s explicit tail calls to dispatch between the go, applyK and applyK' cases, since at that point each function can have the same type signature. I chose the loop and switch method for this post so I can show that defunctionalization can work with any imperative language with a loop construct.

Conclusion

We were able to write expressive code for doing ANF conversion in Standard ML, a functional language, and through a series of mostly mechanical transformations, convert it into stack-safe code in C++. This technique can also be used to generate code in other less-expressive languages like C, Rust, Java, Go, Python, etc. Unlike other methods like trampolining, the resulting code is directly expressed as a loop with little obvious performance pitfalls. I think CPS conversion and defunctionalization are useful techniques to know in order to reliably solve functional programming problems in languages that are more likely to be used in jobs.